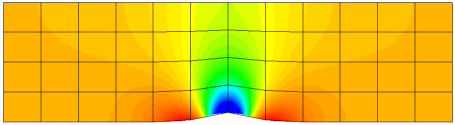
VI2 Smooth Gaussian bump

This problem is aimed at testing high-order methods for the computation of internal flow with a high-order curved boundary representation. In this subsonic flow problem, the geometry is smooth, and so is the flow. Entropy should be a constant in the flow field. The L2 norm of the entropy error is then used as the indicator of solution accuracy since the analytical solution is unknown. The convergence rate can be expected to be P+1, where P is order of the discrete polynomial approximation.

The set of structured quad or triangle grids are generated by the python scripts provided on the web site. The type of meshes, the interpolation order and the number of refinements are specified through options specified at the end of the Smoothbump.py script.